Shader

Shadertoy - 01. Ray Tracing


Shadertoy源码下载

光线追踪，基本思想是从摄像机的位置向屏幕发射光线，然后检测在场景中是否和物体相交

实现思路

  1. 设置参数搭建场景
  2. 发射光线，检测是否和物体相交
  3. 计算最终颜色

因为需要先了解如何检测相交才能决定需要哪些参数，所以先看下如何检测相交

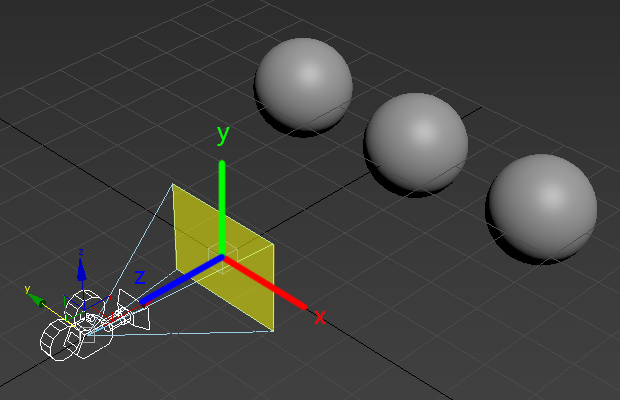
本文坐标系如下，不涉及空间转换
注意： 屏幕坐标系的Z轴正方向应该是垂直于屏幕向里，和图上相反
但是因为后面的光照模型是直接搬的别人的代码，光源位置在轴向向外的情况下显示正常
所以就按照Z轴向外放置摄像机和场景了

如何检测相交

如何检测和球体相交

光线可以用 $ ro+t*rd $ 来表示 ( 光线起始位置 + 长度 * 单位方向向量 )

同时，在球面上的每一点到球心的距离都等于球的半径
所以光线和球的交点必定满足$ | ro + t*rd - center |= R $（ $ ro, rd, center $都是$ vec3 $ ）
为了避免开方的计算，我们把两边都平方，得到$ ( ro + t*rd - center )^2 = R^2 $
这里面$ ro $是摄像机的位置，$ rd $是光线方向，$ center $是球心坐标，$ R $是球的半径
只有$ t $是未知的，是我们需要求解的变量，如果$ t $有解，说明光线和球体相交


重新整理等式，$ [ rd*t + ( ro - center )]^2 = R^2$
展开为$ rd^2t^2 + 2rd( ro - center )t + (ro - center)^2 - R^2 = 0 $
因为$ rd $是单位向量，所以$ rd^2 = 1 $
=> $ t^2 + 2rd( ro - center )t + (ro - center)^2 - R^2 = 0 $


总所周知，一元二次方程的求解公式 $ x = \frac { -b ± \sqrt{b^2-4ac} } { 2a } $
if $ b^2-4ac < 0 $, 无解

1
2
3
4
5
6
7
8
9
10
11
//sph.xyz: center， sph.w: radius
float iSphere(in vec3 ro, in vec3 rd, in vec4 sph)
{
    vec3 oc = ro - sph.xyz;
    float b = dot( oc, rd ); 
    float c = dot(oc,oc) - sph.w*sph.w;
    float h = b*b - c; 
    if( h < 0.0 ) return -1.0;
    float t = -b - sqrt(h);
    return t;
}
如何检测和平面相交

注意这里是指无限大的平面，不是有边界的矩形

我们需要的是xz方向的平面，平面上任意一点可以表示为（0，h，0）
如果相交，光线和平面的交点$P$到平面上任意一点$P_0$的向量必定和平面法线$n$垂直
也就是$PP_0 ·n = 0$
=> $ [ro+t*rd - (0,h,0)] * (0,1,0) = 0 $, 得到 $ t = \frac{h - ro.y}{rd.y} $

1
2
3
4
float iPlane(in vec3 ro, in vec3 rd, in float h) 
{
    return (h-ro.y)/rd.y;
}

设置参数搭建场景

了解如何检测相交之后，我们就知道了要提供哪些参数
$ ro $：摄像机的位置，$ rd $：光线方向，$ center $：球心坐标，$ R $：球的半径

如图所示，$ rd $的集合其实就是这个摄像机视锥，反映了焦距，FOV等
而$ ro $其实是前后移动摄像机以及视锥，等于摄像机和视锥不动，物体前后移动
并不影响透视，镜头拉伸等效果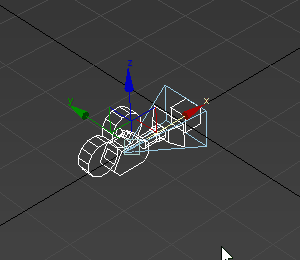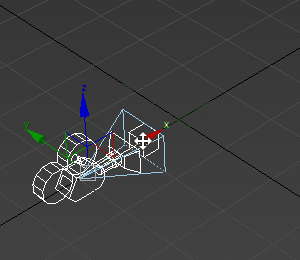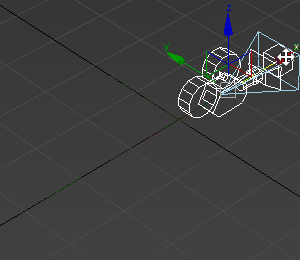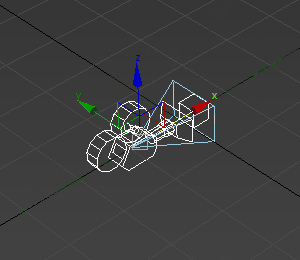

把屏幕坐标转换到[-1,1]，乘以屏幕长宽比确保不会拉伸，这个就是视锥底面的尺寸

1
vec2 uv = (fragCoord * 2.0 - iResolution.xy ) / iResolution.y

而视锥的长度，即$ rd.z $代表了相机的焦距，会影响到最终画面的透视效果

rd.z = 2.14的时候
rd.z = 1.0的时候
这里的2.14是根据Jqx1991的回答模拟人眼透视
视锥角度为25°, 屏幕高度为1，$ \frac {1}{tan25°} ≈ 2.14 $
调节$ rd.z $可以看到透视慢慢转向广角镜头或者鱼眼镜头的效果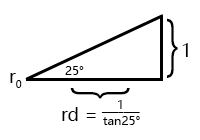

1
vec3 rd = normalize( vec3(uv, -2.14) )

定义球比较简单，$ xyz $是球心坐标，$ w $是半径

1
vec4 s1 = vec4(  0.0, 0.0, -5.0, 1.0 )

计算最终颜色

前面检测相交的函数返回了$ t $
因为是从摄像机发出光线射向屏幕，所以交点一定是在摄像机前面，即$ t >0 $
光线和三个球体以及平面分别进行相交检测，然后得到最小的$ t $值即最近的交点
最开始说过，光线用 $ ro+t*rd $ 来表示，得到$ t $之后代入，得到交点的坐标信息
球体的法线就是从球心到交点向外，平面的法线就是竖直向上
然后进行光照计算得到最终结果，这里直接采用了EKnapik的代码

参考资料

Ray-Tracer
成像视角
光照模型

Share