- 线性变换 linear transform: rotate / scale
- $ f(x) + f(y) = f(x+y) $
- $ kf(x) = f(kx) $
- 仿射变换 affine transform: linear transform + move
- 保持平行线依旧平行,但是长度和角度不一定
OpenGL / DirectX
$$\begin{array}{l|lll}
OpenGL & right-handed & column-major & CBA \vec v \newline
DirectX & left-handed & row-major & \vec v ABC
\end{array}$$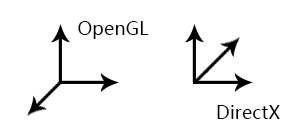
Translation
OpenGL : column-major VS DirectX : row-major
$$
\left[
\begin{array}{cccc}
1 & 0 & 0 & t_x \newline
0 & 1 & 0 & t_y \newline
0 & 0 & 1 & t_z \newline
0 & 0 & 0 & 1
\end{array}
\right]
*
\left[
\begin{array}{c}
x \newline
y \newline
z \newline
1
\end{array}
\right]
or
\left[
\begin{array}{cccc}
x & y & z & 1
\end{array}
\right]
*
\left[
\begin{array}{cccc}
1 & 0 & 0 & 0 \newline
0 & 1 & 0 & 0 \newline
0 & 0 & 1 & 0 \newline
t_x & t_y & t_z & 1
\end{array}
\right]
$$
inverse matrix 逆矩阵: $ T^{-1}(t) = T(-t)$
Rotation
2 dimensions ( OpenGL ) :
$$\begin{bmatrix}
cos\theta & -sin\theta \newline
sin\theta & cos\theta \newline
\end{bmatrix}$$
3 dimensions ( OpenGL ) :
$$R_x(\theta) =
\begin{bmatrix}
1 & 0 & 0 & 0 \newline
0 & cos\theta & -sin\theta & 0 \newline
0 & sin\theta & cos\theta & 0 \newline
0 & 0 & 0 & 1
\end{bmatrix}$$
$$R_y(\theta) =
\begin{bmatrix}
cos\theta & 0 & sin\theta & 0 \newline
0 & 1 & 0 & 0 \newline
-sin\theta & 0 & cos\theta & 0 \newline
0 & 0 & 0 & 1
\end{bmatrix}$$
$$R_z(\theta) =
\begin{bmatrix}
cos\theta & -sin\theta & 0 & 0 \newline
sin\theta & cos\theta & 0 & 0 \newline
0 & 0 & 1 & 0 \newline
0 & 0 & 0 & 1
\end{bmatrix}$$
逆矩阵: $ R_i^{-1}(\theta) = R_i(-\theta)$
for 3x3 rotation mateix, the trace ( the sum of the diagonal elements in a matrix ) is constant :
$ tr(R) = 1+2cos\theta $
Scaling
$$\begin{bmatrix}
S_x & 0 & 0 & 0 \newline
0 & S_y & 0 & 0 \newline
0 & 0 & S_z & 0 \newline
0 & 0 & 0 & 1
\end{bmatrix}$$
逆矩阵: $ S^{-1}(s) = S(\frac{1}{S_x},\frac{1}{S_y},\frac{1}{S_z}) $
- 如果有两项negative = > rotate $ \pi $ radians
- 如果有一项或三项negative => reflection matrix
可能导致incorrect lighting或backface culling,需要先计算行列式determinant是否$<0$
$$
\begin{array}{|lll|}
a_1 & b1 & c1 \newline
a_2 & b2 & c2 \newline
a_3 & b3 & c3 \newline
\end{array}
= a_1b_2c_3 + b_1c_2a_3 + c_1a_2b_3 - a_3b_2c_1 - b_3c_2a_1 - c_3a_2b_1
$$
TRS is the order commonly used( OpenGL ),so S is applied first
其余等用到再看