Shader

Shadertoy - 06. Triangular Prism

1.二维平面的三角形


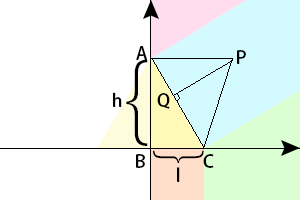
轴对称图案可以通过$|x|$实现，因此只需要着眼于$x$轴正方向的计算推导

  • $P$在红色区域：$d = PA$
  • $P$在蓝色区域：$d = PQ$ 需要求$Q$的位置
  • $P$在绿色区域：$d = PC$
  • $P$在橘色区域：$d = |P.y|$

而$Q$可以用$AQ/AC$的比例$ratio$来表示，$Q = ratio*AC+A ( ration∈[0,1] )$
$ratio = 0$时$Q = A$，$ratio = 1$时$Q=C$
因此，可以合并成两种情况：

  • $P$在红/蓝/绿区域：$d = PQ$
  • $P$在橘色区域： $d = |P.y|$
1.1 $P$在红/蓝/绿区域

$|AQ| = dot( AP, normalize(AC) )$
因为$Q$有可能不在$AC$线段上，所以需要$clamp( |AQ|, 0.0, 1.0 )$
$Q = |AQ|*AC + A, d = |PQ|$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//l:length h:height
float sdTriangle2D(vec2 pos, float l, float h)
{
    vec2 a = vec2(0.0,h);
    vec2 c = vec2(l,0.0);
    vec2 ac = c-a;
    vec2 ap = pos-a;
    
    float aq = dot( ap, normalize(ac) );
    aq = clamp( aq, 0.0, 1.0 ); //ratio    
    
    vec2 q = aq*ac+a;
    
    float pq = length(pos-q); //dist
    return pq;
}

展开带入整理一下可以得到

1
2
3
4
5
6
float sdTriangle2D(vec2 pos, float l, float h)
{
    float ratio = clamp((pos.x*l-pos.y*h+h*h)/(l*l+h*h),0.0,1.0);
    float dist = length(vec2(pos.x-ratio*l,pos.y+ratio*h-h));
    return dist;
}
1.2 判断$P$在红/蓝/绿区域还是橘色区域

橘色区域同时满足两个条件

  • $P.y<0.0$
  • $P.x<l$
1
float mask = step(0.0,l-pos.x)*step(0.0,-pos.y);
1.3 合并两种情况
1
2
3
4
5
6
7
8
float sdTriangle2D(vec2 pos, float l, float h)
{
    float ratio = clamp((pos.x*l-pos.y*h+h*h)/(l*l+h*h),0.0,1.0);
    float dist = length(vec2(pos.x-ratio*l,pos.y+ratio*h-h));
    float mask = step(0.0,l-pos.x)*step(0.0,-pos.y); 
    float d2d = mix(dist,abs(pos.y),mask); 
    return d2d;
}

2.拓展到三维空间


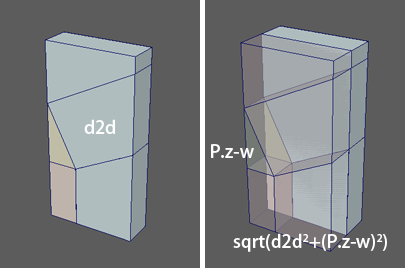
当$P.z<w$的时候，可以直接套用二维空间的公式，$d = d2d = sdTriangle2D(pos,l,h)$
当$P.z>w$的时候，$d = \sqrt{d2d^2+(P.z-w)^2}$，除了垂直于三角锥的空间$d = P.z-w$
而$max(0.0,P.z-w$)可以把$d2d$和$\sqrt{d2d^2+(P.z-w)^2}$合并在一起

  • 垂直于三角锥的空间： $d = P.z-w$
  • 其他：$t = max(0.0, P.z-w); d = \sqrt{t^2 + d2d^2}$
2.1 判断是否是垂直于三角锥的空间

由$A(0.0, h), C(l, 0.0)$可以得到$AC$所在直线的函数$ y = - \frac {h}{l}x+h $
当$ - \frac {h}{l}x+h<y $的时候，说明点在直线下方
同时满足$P.z>0$，就构成了垂直于三角锥的空间

1
mask = step(0.0,h-h/l*pos.x-pos.y)*step(0.0,pos.y);
2.2 合并两种情况
1
2
3
mask = step(0.0,h-h/l*pos.x-pos.y)*step(0.0,pos.y);
float t = max(0.0,pos.z-w);
float d = mix(sqrt(t*t + d2d*d2d),(pos.z-w),mask);
2.3 最终结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
float sdTriangle ( vec3 pos, vec3 offset, float l, float h, float w, float s )
{ 
    pos = pos - offset;
    pos = vec3(abs(pos.x),pos.y,abs(pos.z)); 
    
    float ratio = clamp((pos.x*l-pos.y*h+h*h)/(l*l+h*h),0.0,1.0);    
    float dist = length(vec2(pos.x-ratio*l,pos.y+ratio*h-h));  
    float mask = step(0.0,l-pos.x)*step(0.0,-pos.y); 
    float d2d = mix(dist,abs(pos.y),mask); 

    mask = step(0.0,h-h/l*pos.x-pos.y)*step(0.0,pos.y);
    float t = max(0.0,pos.z-w);
    float d = mix(sqrt(t*t + d2d*d2d),(pos.z-w),mask);
    
    return d-s;//s是边缘倒角
}
Share